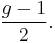Clifford's theorem on special divisors

In mathematics, Clifford's theorem on special divisors is a result of W. K. Clifford on algebraic curves, showing the constraints on special linear systems on a curve C.

If D is a divisor on C, then D is (abstractly) a formal sum of points P on C (with integer coefficients), and in this application a set of constraints to be applied to functions on C (if C is a Riemann surface, these are meromorphic functions, and in general lie in the function field of C). Functions in this sense have a divisor of zeros and poles, counted with multiplicity; a divisor D is here of interest as a set of constraints on functions, insisting that poles at given points are only as bad as the positive coefficients in D indicate, and that zeros at points in D with a negative coefficient have at least that multiplicity. The dimension of the vector space

L(D)

of such functions is finite, and denoted ℓ(D). Conventionally the linear system of divisors attached to D is then attributed dimension r(D) = ℓ(D) − 1, which is the dimension of the projective space parametrizing it.

The other significant invariant of D is its degree, d, which is the sum of all its coefficients.

A divisor is called special if ℓ(K − D) > 0, where K is the canonical divisor.^[1]

In this notation, Clifford's theorem is the statement that for a special divisor D ≠ 0,

ℓ(D) − 1 ≤ d/2,

together with the information that the case of equality here is only for C a hyperelliptic curve, and D an integral multiple of the canonical divisor K.

The Clifford index of C is then defined as the minimum value of the d − 2r(D), taken over all special divisors. Clifford's theorem is then the statement that this is non-negative. The Clifford index for a generic curve of genus g is known to be the floor function of

A conjecture of Mark Green states that the Clifford index for a curve over the complex numbers that is not hyperelliptic should be determined by the extent to which C as canonical curve has linear syzygies. In detail, the invariant a(C) is determined by the minimal free resolution of the homogeneous coordinate ring of C in its canonical embedding, as the largest index i for which the graded Betti number β_{i, i + 2} is zero. Green and Lazarsfeld showed that a(C) + 1 is a lower bound for the Clifford index, and Green's conjecture is that equality always holds. There are numerous partial results.^[2]

References

• E. Arbarello; M. Cornalba, P.A. Griffiths, J. Harris (1985). Geometry of Algebraic Curves Volume I. Grundlehren de mathematischen Wisenschaften 267. ISBN 0-387-90997-4. 

• William Fulton (1974). Algebraic Curves. Mathematics Lecture Note Series. W.A. Benjamin. p. 212. ISBN 0-8053-3081-4. 
• P.A. Griffiths; J. Harris (1994). Principles of Algebraic Geometry. Wiley Classics Library. Wiley Interscience. p. 251. ISBN 0-471-05059-8. 
• Robin Hartshorne (1977). Algebraic Geometry. Graduate Texts in Mathematics. 52. ISBN 0-387-90244-9. 
• Iskovskikh, V.A. (2001), "Clifford theorem", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=C/c022490 

Notes